
 por Fernando Barrichelo
por Fernando Barrichelo
Veja como induzir a cooperação (estratégia 2)
Como resolver o Dilema dos Prisioneiros? Como conseguir a cooperação quando os incentivos induzem as pessoas ao egoísmo e ao individualismo, mesmo sabendo que no final todos perdem? Existem duas formas: a primeira é ter um Regulador Central (como a Lei Cidade Limpa) e a segunda é a estratégia do Olho por Olho em jogos repetitivos. Neste artigo vamos tratar a segunda estratégia. [VER NOTA 1]
Estratégia 2: O Olho por Olho
Em que condições a cooperação surgirá num mundo de egoístas sem uma autoridade central? Essa foi uma das questões em que Robert Axelrod trabalhou para elaborar um estudo que resultou no livro A evolução da cooperação. [VER NOTA 2]
Aqui entra em cena o conceito de reciprocidade ou, como dizem alguns autores, “Você coça minhas costas, depois eu coço a sua”. Eu colaboro com você, então você colabora comigo. Mas sabendo que as pessoas respondem a incentivos e que a recompensa por uma traição é maior, o que garante que eu não vá trair?
Como Axelrod expõe, nas situações em que cada indivíduo tem um incentivo para ser egoísta, como a cooperação pode se desenvolver? A resposta para esse dilema, segundo os cientistas da Teoria dos Jogos, está na repetição infinita das interações entre os jogadores. O que torna possível a cooperação é o fato de os jogadores poderem se encontrar várias vezes. Traduzindo: vou colaborar porque sofrerei retaliação se eu trair, e é melhor você colaborar comigo, pois vou retaliá-lo se você me trair. A traição mútua não é vantajosa para ninguém. Mas o incrível acontece: a retaliação também possui o efeito inverso e promove a cooperação.
O conceito é simples e intuitivo, mas foi sistematizado e provado. O estudo mais conhecido sobre interações repetitivas do jogo do Dilema dos Prisioneiros foi uma competição conduzida por Axelrod em 1980. Ele convidou várias pessoas renomadas das áreas de Teoria dos Jogos, Psicologia, Sociologia, Ciências Políticas e Economia, e propôs estratégias interativas para serem jogadas entre computadores. Os computadores serviam apenas para dar velocidade à simulação (o concurso também poderia ser feito de modo convencional, com várias pessoas presentes, lápis e papel, mas seria muito demorado).
Como definição, estratégia é uma sequência de regras de decisão, é uma especificação do que fazer em qualquer situação que possa surgir. Uma estratégia pode ser cooperar durante algumas jogadas e trair em outras; ela pode usar probabilidades, pode usar o padrão do concorrente e o padrão de resultados para decidir o que fazer em seguida. Nesse concurso, a estratégia deveria especificar o que fazer a cada interação do Dilema dos Prisioneiros e poderia usar todo o histórico de interação. Para cada jogada, o resultado era dado em pontos, como na matriz a seguir.
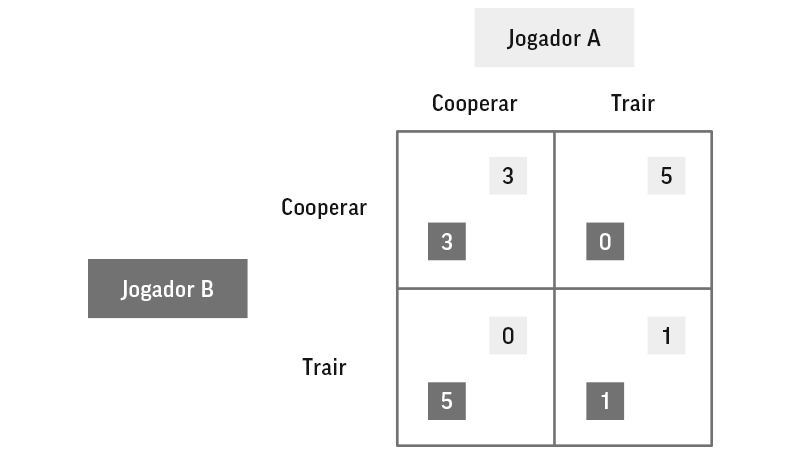
Fig 1 – Matriz de resultados no concurso promovido por Axelrod
Esse esquema de pontuação lembra a matriz do Dilema dos Prisioneiros. Duas pessoas participam de um jogo. Elas precisam escolher entre duas opções: Cooperar ou Trair. As possíveis combinações são:
- Se ambas cooperarem, cada uma ganha 3 pontos como Recompensa.
- Se ambas traírem, cada uma ganha 1 ponto, que é a Punição por não cooperar.
- Se uma trair enquanto a outra cooperar, a traidora recebe 5 pontos (que é a Tentação) e a colaboradora não recebe nada (é a Inocente).
Como um jogador racional irá jogar? Traindo, é claro. Essa é a resposta correta, como vimos anteriormente, não importando o que o outro vai fazer, porque:
- Se o outro jogador vai Cooperar, então você ganha 5 pontos ao Trair ou 3 pontos ao Cooperar. Melhor Trair.
- Se o outro jogador vai Trair, então você ganha 1 ponto ao Trair ou 0 pontos ao Cooperar. Melhor Trair.
O problema é que o outro jogador, sendo racional, pensa exatamente da mesma forma. Como resultado, ambos acabam ganhando apenas 1 ponto, muito menos do que se houvesse a cooperação mútua, pois assim poderiam ganhar 3 pontos cada. Como Karl Sigmund afirma, o Dilema dos Prisioneiros não é, de fato, um dilema, pois trair é a única opção racional. Então, como conseguir a cooperação? A resposta está na repetição do jogo, como foi demonstrado no concurso. [VER NOTA 3]
No torneio conduzido por Axelrod, cada programa competia com todos os outros programas (inclusive com ele mesmo), e os pontos eram acumulativos. Cada jogo consistia em 200 jogadas. Como era possível ganhar 5 pontos em cada jogada, teoricamente a pontuação final variava de 0 a 1.000. Por exemplo: quando uma estratégia “Sempre Cooperar” joga contra uma estratégia “Sempre Trair”, quem Cooperar soma 0 pontos e quem Trair soma 1.000 pontos. Uma pontuação razoável é ganhar três em cada uma das 200 interações, quando ambos cooperam toda vez, somando 600 pontos.
Importante: Não há uma estratégia certa, pois tudo depende do adversário com que você está jogando. Colaborar é uma coisa; somar mais pontos é outra. Assim, nenhuma estratégia é melhor, independentemente da estratégia do outro. Por exemplo, se você jogar contra um programa que sempre colabora, sua melhor estratégia é trair sempre, pois conseguirá 5 pontos todas as vezes.
O problema é que nem sempre você sabe contra quem está jogando; não é porque seu oponente cooperou duas vezes que ele irá cooperar em todas as demais jogadas. O inverso também é verdade: se você encontrar um jogador que sempre trai, então melhor trair, pois ao menos você consegue um ponto no lugar de zero. Você não quer ser o inocente (ganhar zero), enquanto seu adversário ganha ao trair.
Jogar contra um jogador que sempre colabora ou sempre trai é muito simples. Mas, na prática, seu oponente reage conforme a sua jogada e conforme as crenças que ele tem sobre você. Além disso, o concurso não esperava encontrar a estratégia mais bondosa, mais ética. O que ele esperava era descobrir qual estratégia somaria mais pontos, considerando que os jogadores não podiam se comunicar e que levavam em conta, a cada momento, as decisões do passado como aprendizado.
Nesse primeiro concurso, 14 estratégias foram inscritas. Axelrod acrescentou mais um jogador com uma estratégia “aleatória” (50% de chance entre Cooperar e Trair). A estratégia mais longa das inscritas teve 77 linhas de código de programa e obteve o pior resultado: 282,2 pontos em média. A estratégia aleatória foi um pouco pior: 276,3 pontos.
A estratégia vencedora: Olho por Olho
A estratégia com maior pontuação foi também a estratégia mais simples. Enviada por Anatol Rapopor, foi chamada de Olho por Olho (em inglês, tit for tat) . Ela tinha quatro linhas de código e pode ser explicada numa sentença: coopere na primeira jogada, depois faça o que o outro jogador fez na jogada anterior.
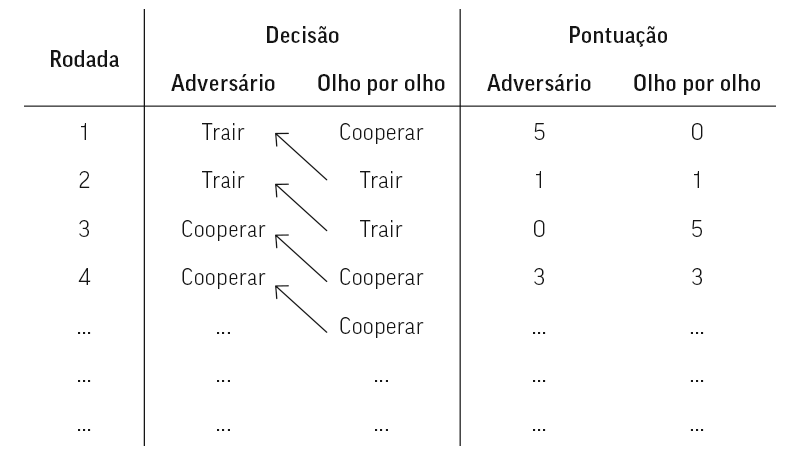
Fig 2 – Simulação passo a passo em um jogo com Olho por Olho
Olho por Olho fez em média 504,5 pontos. Em todas as jogadas, suas pontuações variaram de 225 a 600 pontos, pontuação máxima possível. Por que a estratégia Olho por Olho é tão efetiva? William Poundstone explica bem o sucesso dela por meio de cinco motivos: [VER NOTA 4 e 5]
- Primeiro, é uma estratégia gentil, pois nunca é a primeira a trair. Ela começa colaborando e dá ao oponente o benefício da dúvida. Se a outra estratégia retornar o favor e continuar assim, Olho por Olho nunca trai. Ela não arranja encrenca e fica contente se assim continuar. Quando Olho por Olho joga contra si mesmo, ambos começam cooperando e nunca provocam o outro. Para se ter noção, os oito primeiros classificados tinham uma estratégia gentil, ou seja, nunca eram o primeiro a trair. Os outros não. As estratégias gentis pontuaram entre 472 e 504 pontos, enquanto a estratégia não gentil mais bem classificada obteve 401 pontos. Assim, não ser o primeiro a trair era uma propriedade que separava as estratégias mais bem-sucedidas das menos bem-sucedidas.
- Segundo, Olho por Olho também é provocativa. Ela trai em resposta a uma traição. Depois da segunda rodada, ela responde à provocação do outro na mesma moeda. Se a outra estratégia trai na jogada 5, então Olho por Olho trai na rodada 6.
- Terceiro, outro grande predicado de Olho por Olho é o perdão. Ela não é draconiana a ponto de uma simples transgressão levar à traição perpétua. Sempre está disposta a cooperar à medida que o oponente queira cooperar. Se a outra estratégia cooperar, então Olho por Olho volta a cooperar também.
- Quarto, além de ser gentil, provocativa e disposta ao perdão, Olho por Olho é uma estratégia simples. Ela diz “Faça ao outro o que ele faz a você”. A ameaça faz parte do seu comportamento estratégico, e Olho por Olho cumpre a promessa ao repetir a ação mais recente do oponente na esperança de que a outra estratégia perceba isso. Interessante é que Olho por Olho pune a traição do adversário de imediato, na jogada seguinte. Essa estratégia mostra-se melhor que outras, do tipo “Contar até dez antes de ficar zangado” (ou seja, deixar passar um certo número de traições antes de retaliar).
- Quinto, mais uma qualidade importante do Olho por Olho é que sua estratégia é transparente. Alguém jogando Olho por Olho não precisa ter medo de que o oponente descubra sua estratégia. Pelo contrário, é bom que o oponente saiba disso. Quando se joga contra Olho por Olho, ninguém pode se sair melhor do que se cooperar. Isso faz dela uma estratégia muito estável.
O primeiro concurso de Axelrod não foi tão conclusivo porque forem inscritos apenas 14 programas, não representando, portanto, todas as estratégias possíveis. Por isso, Axelrod promoveu um segundo concurso e informou o resultado do primeiro e o sucesso do Olho por Olho. Estava implícito que agora o desafio era vencer esta estratégia. No total, foram inscritos 62 programas de seis países. Apesar da forte concorrência, Olho por Olho venceu novamente.
O mais interessante é que Olho por Olho ganhou sem explorar nenhuma outra estratégia. Além disso, não venceu ninguém em particular, mas mesmo assim ganhou o concurso. As estratégias foram chamadas para competir, e não para colaborar. Ou seja, o objetivo era somar mais pontos, mesmo que fosse preciso trair. Não havia julgamento moral; trair fazia parte legítima do jogo. E o intrigante é que a estratégia vencedora, Olho por Olho, prega a colaboração; quem mais colaborou ganhou mais pontos, somando todos os jogos.
O próprio Axelrod, em seu livro, conclui: [VER NOTA 6]
Olho por Olho venceu o torneio porque ele foi bom em suas interações com uma grande variedade de outras estratégias. Em média, foi melhor do que qualquer outra regra; no entanto, Olho por Olho não pontuou melhor que seu adversário em nenhum jogo. Na verdade, ele não pode. Ele deixa o outro jogador trair primeiro e nunca escolhe trair mais vezes que os outros jogadores. Portanto, Olho por Olho atinge sempre a mesma pontuação que o outro jogador ou um pouco menos. Olho por Olho venceu o concurso não por ganhar dos outros jogadores, mas forçando o comportamento do outro jogador e deixando-o fazer o bem. Olho por Olho foi tão consistente em proporcionar resultados mutuamente gratificantes que alcançou maior pontuação geral do que qualquer outra estratégia.
Em resumo, a estratégia Olho por Olho educa o oponente para a cooperação. Na vida real, se você trair, na próxima rodada seu oponente irá traí-lo e criar uma situação indesejável. Por isso, você tem incentivos para colaborar e dar o exemplo para que nas próximas interações vocês consigam uma situação ganha-ganha. Mas se você cooperar para dar o exemplo, e ele trair para se aproveitar da situação? Daí você retribui com uma retaliação na sequência. Se ele colaborar, você perdoa e volta a colaborar.
De certa forma, essa foi a dinâmica na época da Guerra Fria, segundo Robert Aumann (mais detalhes nos apêndices). O medo da retaliação trouxe a paz – com medo de iniciar uma guerra nuclear, os Estados Unidos não atacaram a Rússia, e vice-versa. Segundo Aumann, se um deles não tivesse o poder de retaliação, o outro teria atacado e a paz não existiria.
Olho por Olho funciona apenas em jogos repetitivos
Para que essa dinâmica funcione e induza à cooperação é preciso estar em um jogo em que as interações sejam repetidas. Mas será mesmo que a simples repetição das interações leva à cooperação? Karl Sigmund defende a ideia de que se o número de interações é conhecido com antecedência por ambos os jogadores, não haverá cooperação. [VER NOTA 7]
Por quê? Porque a última rodada da série é, na verdade, o simples Dilema dos Prisioneiros de uma jogada só, e o resultado já é conhecido: a traição, pois não haverá próxima oportunidade para sofrer a retaliação. Nessa última interação, trair não traz consequência de retaliação e não afetará as próximas rodadas (que não existirão). Uma vez que a última interação já está definida (Trair), o que acontecerá na penúltima jogada? A mesma coisa (Trair), pois não há incentivo para colaborar se você sabe que o adversário vai trair pelo mesmo raciocínio – a penúltima jogada tem as mesmas características da última jogada. Revendo o raciocínio em todas as jogadas, descobre-se que não haverá colaboração em nenhum ponto se ambos pensarem racionalmente. Sabendo que o adversário deve trair, não há motivos para colaborar.
E então nunca existirá cooperação? Pode existir, pois em um jogo repetido é a expectativa de futuros encontros que faz a cooperação ser mais atraente. O fim das interações não deve ser conhecido com antecedência; deve sempre existir alguma probabilidade de uma próxima jogada. Esse é o significado da expressão “O mundo dá voltas”, e o poder educativo de deixar claro a estratégia Olho por Olho: “Você coça as minhas costas e eu coço as suas, mas se você trair, saiba que o mundo dá voltas; voltaremos a nos encontrar e revidarei com traição. Então, é melhor colaborar desde já”.
O dilema da gorjeta – repetitivo ou uma vez?
Acabamos de mostrar um raciocínio no mundo da Teoria dos Jogos em que a cooperação ocorre quando há interações repetidas e, particularmente, quando não se sabe qual será a última vez. Por outro lado, numa situação estilo Dilema dos Prisioneiros de apenas uma jogada, a melhor estratégia racional é trair, uma vez que não há uma nova chance para o outro revidar.
Agora vamos raciocinar com o exemplo de um restaurante em que a gorjeta é opcional. Não se trata de um Dilema dos Prisioneiros típico, no qual “o melhor racional individual é o pior coletivo”, mas a analogia com situações repetidas versus interação única se encaixa bem neste dilema da gorjeta.
Há tempos que os economistas se perguntam por que as pessoas dão gorjetas. Existem duas explicações possíveis. A primeira, mais emocional, refere-se ao sentimento de que o garçom recebe salário fixo muito baixo e depende de gorjetas para complementar a renda; assim, há uma atitude altruísta de agradecimento e colaboração.
A segunda explicação racional dessa “generosidade” está exatamente no autointeresse do cliente nas interações repetidas – frequentadores assíduos dão gorjetas mais polpudas justamente porque os garçons irão atendê-los cada vez melhor. Se dar gorjeta para receber um bom serviço na próxima vez é um raciocínio válido, imagine o inverso. Se você não der gorjeta, alguns garçons ficam revoltados e vingativos. É preciso tomar cuidado com algumas reações. Por isso, suponha que você é um frequentador assíduo de um restaurante e nunca dá gorjeta. Provavelmente o garçom se lembrará de você na próxima vez. Essa é uma situação de interação repetida que pede cuidado com garçons e cozinheiros vingativos. É o típico olho por olho, dente por dente.
Entretanto, se você está viajando e sabe que possivelmente não voltará àquele restaurante, por qual razão daria gorjeta? Igualmente, por que dar dinheiro a mais ao taxista ou à camareira? Do ponto de vista racional econômico no mundo do autointeresse, não há razão para cooperar (gastar mais) em uma situação de jogada única.
A prática da gorjeta contraria os pressupostos da economia clássica. Afinal, a gorjeta é uma despesa que os consumidores podem evitar, e o pagamento é realizado após o serviço feito, portanto sem vínculo com a qualidade. Mesmo assim, percebe-se que as pessoas deixam gorjetas, mesmo quando nunca mais retornarão. Acadêmicos recorrem às normas sociais, e não econômicas, para explicar esse fenômeno, uma vez que já virou uma prática quase universal.
Recapitulando
O Dilema dos Prisioneiros apresenta um esquema de incentivos que induz à traição quando jogado uma única vez – os prisioneiros nunca mais vão se ver (ou o jogo acabou). É por isso que fazemos a analogia com o Dilema da Confiança: sem poder confiar e com apenas uma jogada a fazer, a traição é mais segura, mesmo ganhando menos se o outro trair também. A solução para esse caso é ter uma autoridade central que regule os comportamentos.
Já em um jogo repetitivo ou infinito, a traição é, na verdade, um instrumento para sinalizar que haverá retaliação, caso o outro traia. Então, com o tempo, ambos acabam aprendendo a colaborar, pois isso confere a todos mais benefícios. Alguns cientistas da Teoria dos Jogos e biólogos usam esse raciocínio para explicar como, na evolução humana, a colaboração foi conquistada e praticada.
O torneio de Axelrod forneceu provas bem razoáveis nesse sentido após mostrar que a estratégia Olho por Olho somou mais pontos nos dois torneios ao jogar contra uma série de outras estratégias. Foram cinco os atributos dessa estratégia: gentileza, provocação, perdão, simplicidade e transparência. E, é claro, para ser efetiva, a estratégia Olho por Olho apenas funciona quando há a expectativa de que o jogo vá continuar indefinitivamente, como é a vida real (“O mundo dá voltas”).



Comentários